Laboratory 4 - Estimation, filtering and system identification - Prof. M. Taragna
Exercise: Design of Kalman predictors and filters for a LTI dynamic system
Contents
Introduction
The program code may be splitted in sections using the characters "%%". Each section can run separately with the command "Run Section" (in the Editor toolbar, just to the right of the "Run" button). You can do the same thing by highlighting the code you want to run and by using the button function 9 (F9). This way, you can run only the desired section of your code, saving your time. This script can be considered as a reference example.
clear all, close all, clc
Procedure
- Load the file data.mat containing the input signal
- Define the LTI dynamic system S
- Define the noise variances
- Set the initial state of the LTI dynamic system S
- Simulate the LTI dynamic system S
- Plot states and output of the LTI dynamic system S
- Initialize the dynamic predictor K
- Simulate the dynamic predictor K and the filter F
- Compute the RMSEs for the dynamic predictor K and the filter F
- Plot the estimated states and output versus the actual ones
- Initialize the steady-state predictor Kinf
- Simulate the steady-state predictor Kinf and the filter Finf
- Compute the RMSEs for the steady-state predictor Kinf and the filter Finf
- Plot the estimated states and output versus the actual ones
- (Optional) Initialize the dynamic predictor Kpc
- (Optional) Simulate the dynamic predictor Kpc
Problem setup
% Step 1: load of data load data % u = input signal, computed as: sign(sin(2*pi*0.0005*(1:4000)))*1+10; N=length(u); % N = number of data N0_vector=[0, 20, 100]; % Step 2: definition of LTI dynamic system S A=[ 0.96, 0.5, 0.27, 0.28; ... -0.125, 0.96, -0.08, -0.07; ... 0, 0, 0.85, 0.97; ... 0, 0, 0, 0.99]; B=[1; -1; 2; 1]; C=[0, 2, 0, 0]; D=[0]; % Note that: A is stable, (A,C) is observable % Step 3: definition of noise variances Bv1=sqrt(15)*[0.5; 0; 0; 1]; % Note that: (A,Bv1) is reachable V1=Bv1*Bv1'; V2=2000; V12=0; rng('default'); % To produce the same random numbers at each run
LTI dynamic system simulation
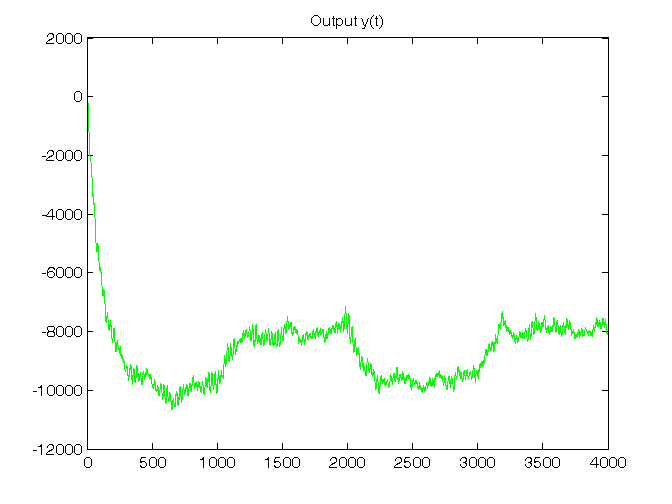
% Step 4: LTI dynamic system initialization x(:,1)=[30; 40; -70; -10]; [n,nn]=size(A); % Step 5: LTI dynamic system simulation for t=1:N, % noises v1(:,t)=mvnrnd(zeros(1,n),Bv1*Bv1')'; v2(t)=sqrt(V2)*randn; % system x(:,t+1)=A*x(:,t)+B*u(t)+v1(:,t); y(t)=C*x(:,t)+D*u(t)+v2(t); end Cov_v1=cov(v1'), V1 % To verify that: Var(v1) approximates V1 Cov_v2=cov(v2'), V2 % To verify that: Var(v2) approximates V2 % Step 6: plot of LTI system states and output T=1:N; for k=1:n, figure, plot(T,x(k,1:N),'g'), title(['State x_',num2str(k),'(t)']) end figure, plot(T,y(1:N),'g'), title('Output y(t)')
Cov_v1 =
3.8177 0 0 7.6353
0 0 0 0
0 0 0 0
7.6353 0 0 15.2707
V1 =
3.7500 0 0 7.5000
0 0 0 0
0 0 0 0
7.5000 0 0 15.0000
Cov_v2 =
1.9130e+03
V2 =
2000
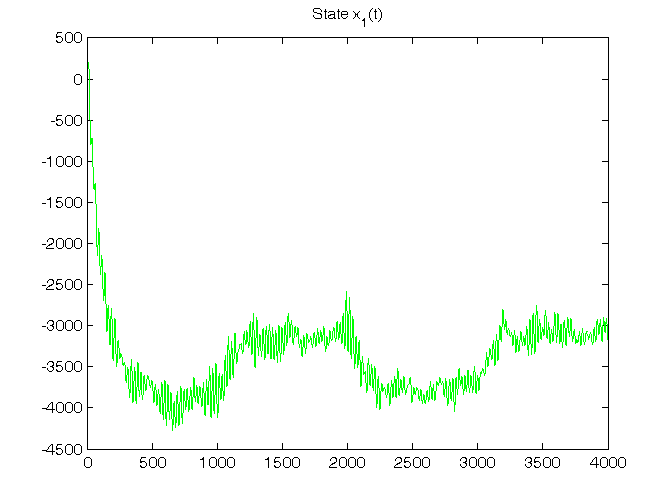
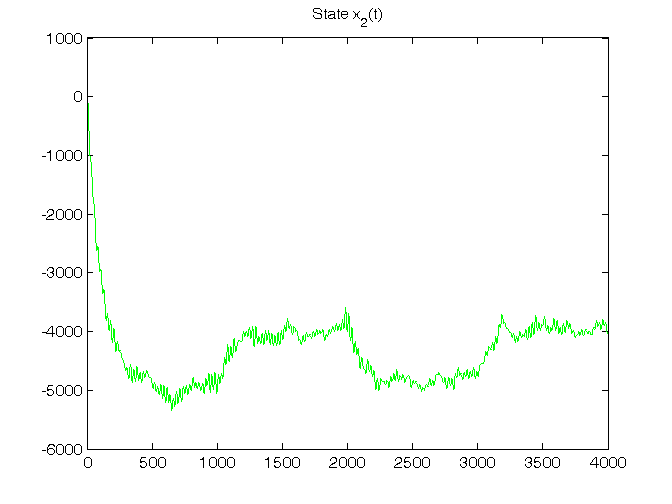
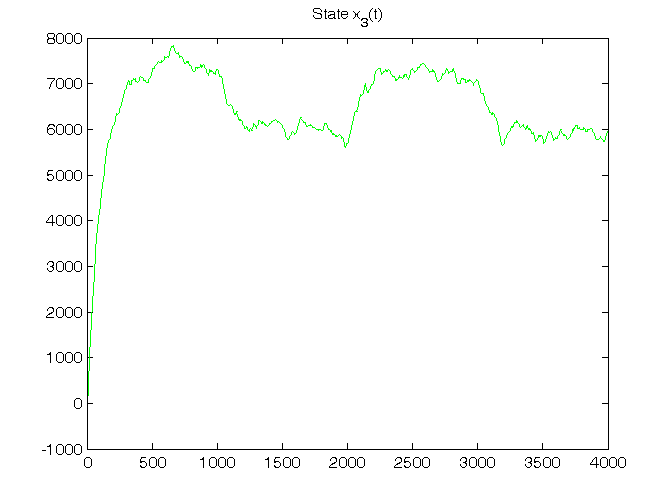
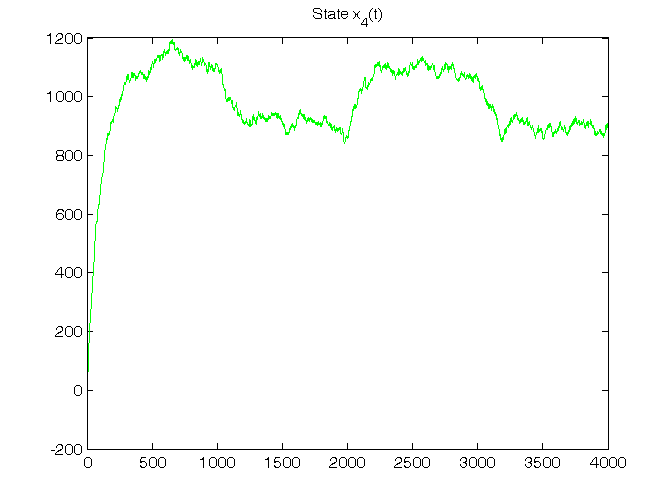
Dynamic predictor K and filter F in standard form
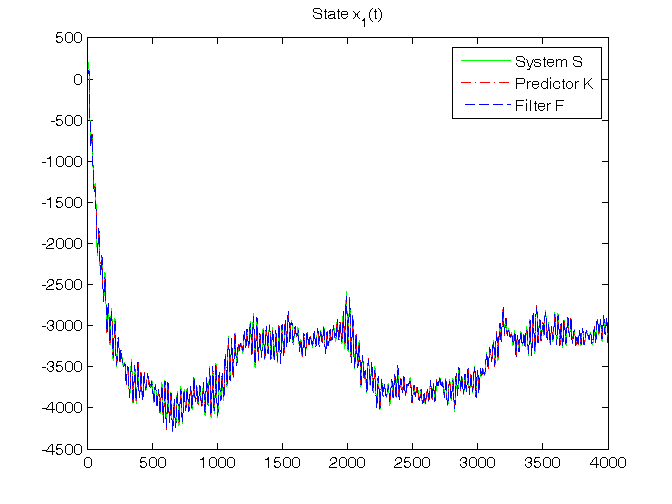
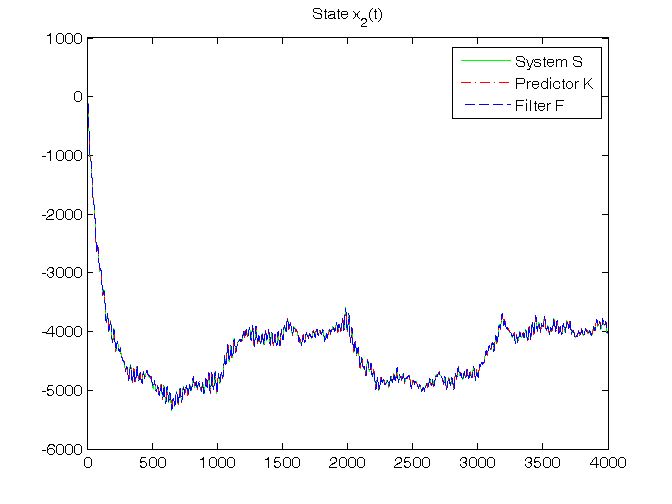
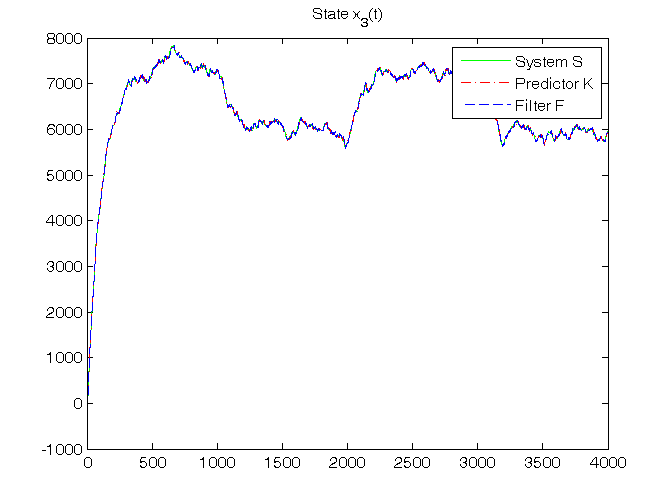
% Step 7: dynamic predictor K initialization x_h(:,1)=zeros(n,1); P{1}=0.5*eye(n); % Step 8: dynamic predictor K and filter F simulation for t=1:N, % dynamic predictor K y_h(t)=C*x_h(:,t); e(t)=y(t)-y_h(t); K{t}=(A*P{t}*C'+V12)*inv(C*P{t}*C'+V2); x_h(:,t+1)=A*x_h(:,t)+B*u(t)+K{t}*e(t); P{t+1}=A*P{t}*A'+V1-K{t}*(C*P{t}*C'+V2)*K{t}'; % dynamic filter F K0{t}=P{t}*C'*inv(C*P{t}*C'+V2); x_f(:,t)=x_h(:,t)+K0{t}*e(t); y_f(t)=C*x_f(:,t); end K_N=K{N} K0_N=K0{N} % Step 9: RMSE computation for ind=1:length(N0_vector), N0=N0_vector(ind); for k=1:n, RMSE_x_h(k,ind)=norm(x(k,N0+1:N)-x_h(k,N0+1:N))/sqrt(N-N0); RMSE_x_f(k,ind)=norm(x(k,N0+1:N)-x_f(k,N0+1:N))/sqrt(N-N0); end RMSE_y_h(ind)=norm(y(N0+1:N)-y_h(N0+1:N))/sqrt(N-N0); RMSE_y_f(ind)=norm(y(N0+1:N)-y_f(N0+1:N))/sqrt(N-N0); end fprintf('\n N0 = %d N0 = %d N0 = %d\n',N0_vector(1),N0_vector(2),N0_vector(3)) RMSE_x_h, RMSE_y_h, RMSE_x_f, RMSE_y_f % Step 10: graphical comparison of the results for k=1:n, figure, plot(T,x(k,1:N),'g', T,x_h(k,1:N),'r-.', T,x_f(k,1:N),'b--'), title(['State x_',num2str(k),'(t)']), legend('System S','Predictor K','Filter F') end figure, plot(T,y(1:N),'g', T,y_h(1:N),'r-.', T,y_f(1:N),'b--'), title('Output y(t)'), legend('System S','Predictor K','Filter F')
K_N =
-0.2008
0.2352
-0.2881
-0.0634
K0_N =
-0.2148
0.1902
-0.2659
-0.0640
N0 = 0 N0 = 20 N0 = 100
RMSE_x_h =
27.8311 27.5715 27.3745
16.8500 16.7117 16.7443
28.8517 28.7171 28.7069
10.1058 10.0767 10.0442
RMSE_y_h =
56.1359 55.7381 55.6878
RMSE_x_f =
25.0575 24.7751 24.6337
13.2025 13.0715 13.1061
24.6422 24.5131 24.5315
9.3866 9.3601 9.3394
RMSE_y_f =
35.0983 34.5311 34.4994
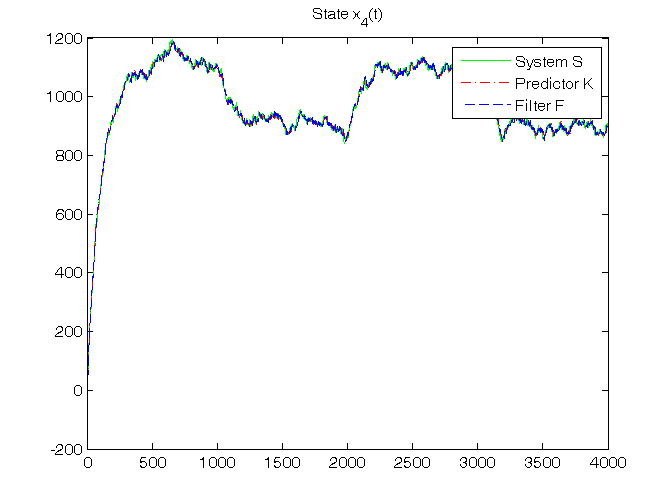
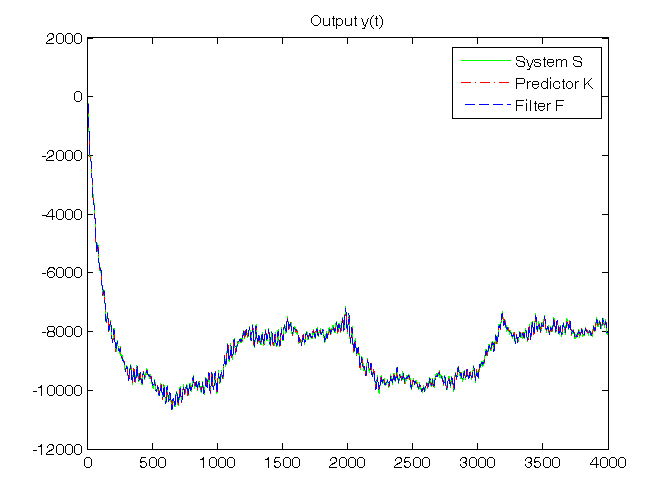
Steady-state predictor Kinf and filter Finf in standard form
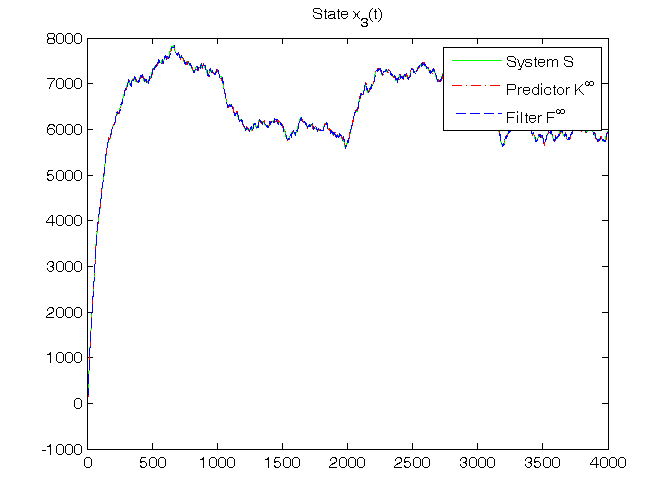
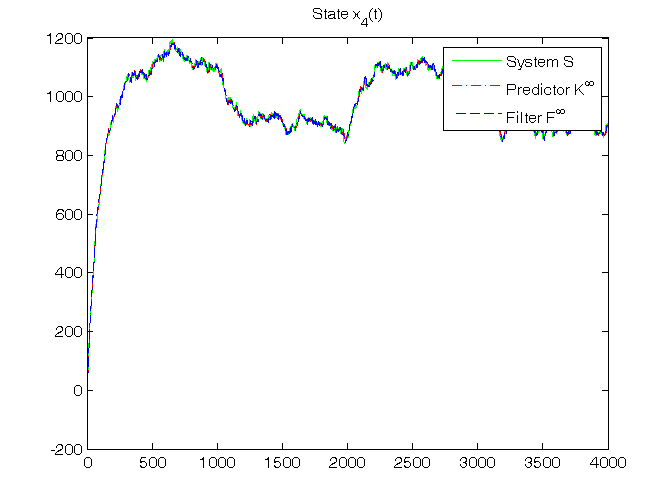
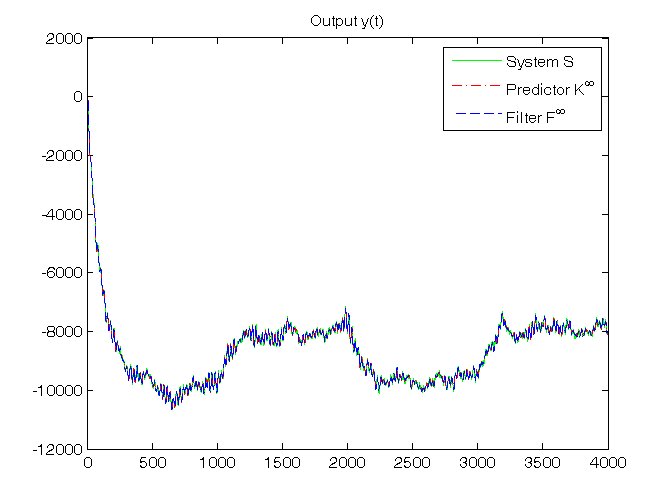
% Step 11: steady-state predictor Kinf initialization x_h_ss(:,1)=zeros(n,1); % Off-line computation of steady-state Kalman gain matrices Sys1=ss(A,[B, eye(n)],C,[D, zeros(1,n)],1); [Kalman_predictor,Kbar,Pbar,K0bar]=kalman(Sys1,V1,V2,0); Kbar % To verify that: Kbar = K_N K0bar % To verify that: K0bar = K0_N A_K0bar=A*K0bar % To verify that: Kbar = A*K0bar % Step 12: steady-state predictor Kinf and filter Finf simulation for t=1:N, % steady-state predictor Kinf y_h_ss(t)=C*x_h_ss(:,t); e_ss(t)=y(t)-y_h_ss(t); x_h_ss(:,t+1)=A*x_h_ss(:,t)+B*u(t)+Kbar*e_ss(t); % steady-state filter Finf x_f_ss(:,t)=x_h_ss(:,t)+K0bar*e_ss(t); y_f_ss(t)=C*x_f_ss(:,t); end % Step 13: RMSE computation for ind=1:length(N0_vector), N0=N0_vector(ind); for k=1:n, RMSE_x_h_ss(k,ind)=norm(x(k,N0+1:N)-x_h_ss(k,N0+1:N))/sqrt(N-N0); RMSE_x_f_ss(k,ind)=norm(x(k,N0+1:N)-x_f_ss(k,N0+1:N))/sqrt(N-N0); end RMSE_y_h_ss(ind)=norm(y(N0+1:N)-y_h_ss(N0+1:N))/sqrt(N-N0); RMSE_y_f_ss(ind)=norm(y(N0+1:N)-y_f_ss(N0+1:N))/sqrt(N-N0); end fprintf('\n N0 = %d N0 = %d N0 = %d\n',N0_vector(1),N0_vector(2),N0_vector(3)) RMSE_x_h_ss, RMSE_y_h_ss, RMSE_x_f_ss, RMSE_y_f_ss % Step 14: graphical comparison of the results for k=1:n, figure, plot(T,x(k,1:N),'g', T,x_h_ss(k,1:N),'r-.', T,x_f_ss(k,1:N),'b--'), title(['State x_',num2str(k),'(t)']), legend('System S','Predictor K^\infty','Filter F^\infty') end figure, plot(T,y(1:N),'g', T,y_h_ss(1:N),'r-.', T,y_f_ss(1:N),'b--'), title('Output y(t)'), legend('System S','Predictor K^\infty','Filter F^\infty')
Kbar =
-0.2008
0.2352
-0.2881
-0.0634
K0bar =
-0.2148
0.1902
-0.2659
-0.0640
A_K0bar =
-0.2008
0.2352
-0.2881
-0.0634
N0 = 0 N0 = 20 N0 = 100
RMSE_x_h_ss =
27.6086 27.5865 27.3745
16.7265 16.6999 16.7443
28.7560 28.7026 28.7069
10.0886 10.0766 10.0442
RMSE_y_h_ss =
55.8566 55.7238 55.6878
RMSE_x_f_ss =
24.8505 24.7931 24.6337
13.0924 13.0657 13.1061
24.5320 24.5037 24.5315
9.3721 9.3600 9.3394
RMSE_y_f_ss =
34.6039 34.5216 34.4994
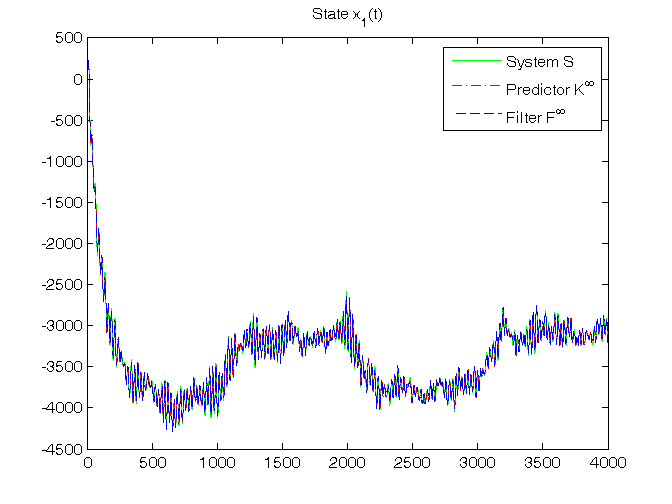
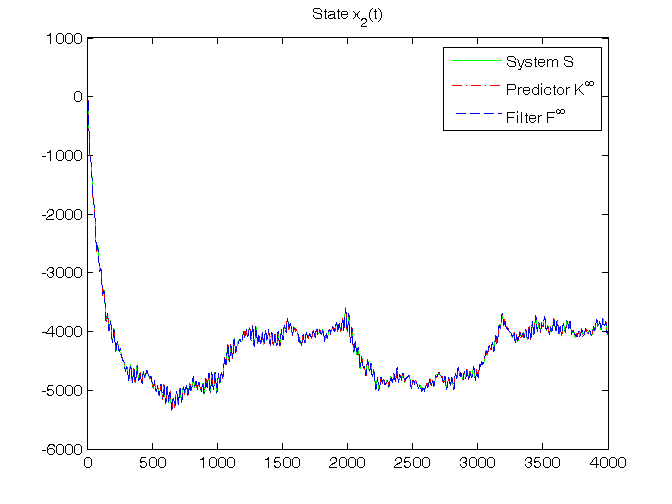
(Optional) Dynamic predictor Kpc in predictor-corrector form
% Step 15: dynamic predictor Kpc initialization x_h_pc(:,1)=zeros(n,1); P{1}=0.5*eye(n); % Step 16: dynamic predictor Kpc simulation for t=1:N, K0{t}=P{t}*C'*inv(C*P{t}*C'+V2); P0{t}=(eye(n)-K0{t}*C)*P{t}; P{t+1}=A*P0{t}*A'+V1; y_h_pc(t)=C*x_h_pc(:,t); e_pc(t)=y(t)-y_h_pc(t); x_f_pc(:,t)=x_h_pc(:,t)+K0{t}*e_pc(t); x_h_pc(:,t+1)=A*x_f_pc(:,t)+B*u(t); end norm(x_h-x_h_pc,inf) % To verify that: Kpc = K norm(x_f-x_f_pc,inf) % To verify that: Fpc = F
ans = 1.0246e-08 ans = 9.3451e-09