Esercitazione di laboratorio #6 - Controlli Automatici
Esercizio #2
Autori: M. Indri, M. Taragna (ultima modifica: 17/05/2020)
Contents
- Comandi di pulizia iniziali
- Definizione del sistema
- Punto a): studio di F(s)
- Punti b) e c): studio di Ga(s) per Kc = 1
- Punto d): calcolo di W(s) e dei suoi poli per Kc = -0.1 dopo studio della stabilità
- Punto e): errore di inseguimento in regime permanente
- Caso e.1): r(t)=t, d1(t)=0.1, d2(t)=0.5
- Caso e.2): r(t)=2, d1(t)=0.1, d2(t)=0.01t
Comandi di pulizia iniziali
clear all, close all
Definizione del sistema
s=tf('s');
F=(s-1)/((s+0.2)*(s^3+2.5*s^2+4*s))
F =
s - 1
-------------------------------
s^4 + 2.7 s^3 + 4.5 s^2 + 0.8 s
Continuous-time transfer function.
Punto a): studio di F(s)
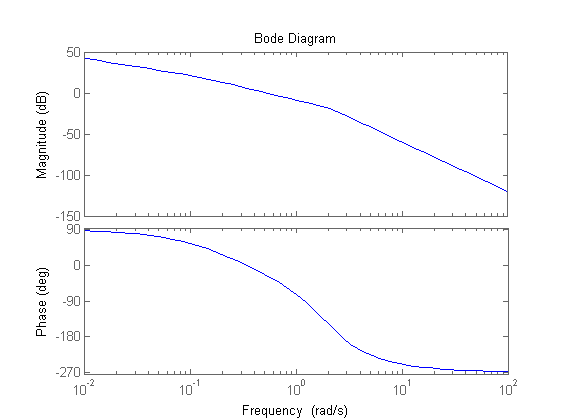
% Guadagno stazionario di F(s) Kf=dcgain(s*F) % F(s) ha 1 polo nell'origine % Zeri e poli di F(s) zeri=zero(F) poli=pole(F) damp(F) % Diagrammi di Bode di F(jw)(valutazione fase iniziale e finale) bode(F)
Kf =
-1.2500
zeri =
1
poli =
0.0000 + 0.0000i
-1.2500 + 1.5612i
-1.2500 - 1.5612i
-0.2000 + 0.0000i
Pole Damping Frequency Time Constant
(rad/seconds) (seconds)
0.00e+00 -1.00e+00 0.00e+00 Inf
-2.00e-01 1.00e+00 2.00e-01 5.00e+00
-1.25e+00 + 1.56e+00i 6.25e-01 2.00e+00 8.00e-01
-1.25e+00 - 1.56e+00i 6.25e-01 2.00e+00 8.00e-01
Punti b) e c): studio di Ga(s) per Kc = 1
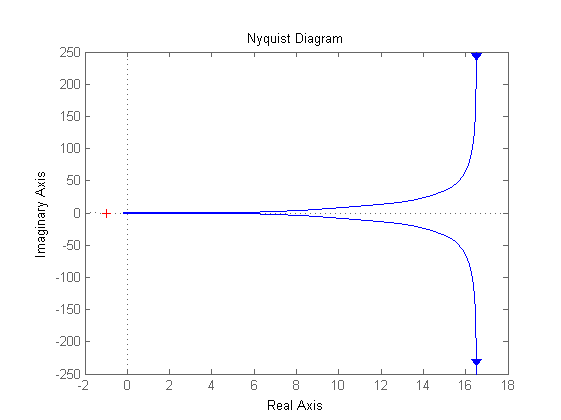
Kc = 1 Kr=0.5 Ga1=Kc*F/Kr % Diagrammi di Bode di Ga1(jw) figure, bode(Ga1) % Diagramma di Nyquist di Ga1(jw), da ingrandire opportunamente % in corrispondenza degli attraversamenti dell'asse reale % (in +4, -0.109 e 0) figure, nyquist(Ga1) w=logspace(-1,3,5000); figure,nyquist(Ga1,w)
Kc =
1
Kr =
0.5000
Ga1 =
s - 1
-------------------------------------
0.5 s^4 + 1.35 s^3 + 2.25 s^2 + 0.4 s
Continuous-time transfer function.


Punto d): calcolo di W(s) e dei suoi poli per Kc = -0.1 dopo studio della stabilità
% Dallo studio della stabilità in catena chiusa con il criterio di Nyquist: % n_ia = 0 % n_ic = 1 per 0 < Kc < 9.17 % n_ic = 3 per Kc > 9.17 % n_ic = 0 (asintotica stabilità) per -0.25 < Kc < 0 % n_ic = 2 per Kc < -0.25 Kc=-0.1 Ga=Kc*F/Kr; W=feedback(Kc*F,1/Kr) damp(W)
Kc =
-0.1000
W =
-0.1 s + 0.1
-------------------------------------
s^4 + 2.7 s^3 + 4.5 s^2 + 0.6 s + 0.2
Continuous-time transfer function.
Pole Damping Frequency Time Constant
(rad/seconds) (seconds)
-5.72e-02 + 2.12e-01i 2.61e-01 2.19e-01 1.75e+01
-5.72e-02 - 2.12e-01i 2.61e-01 2.19e-01 1.75e+01
-1.29e+00 + 1.58e+00i 6.34e-01 2.04e+00 7.74e-01
-1.29e+00 - 1.58e+00i 6.34e-01 2.04e+00 7.74e-01
Punto e): errore di inseguimento in regime permanente
Nota bene: il sistema di controllo e' di tipo 1
We=Kr*feedback(1,Ga) Wd1=feedback(F,Kc/Kr) Wd2=feedback(1,Ga)
We =
0.25 s^4 + 0.675 s^3 + 1.125 s^2 + 0.2 s
-------------------------------------------
0.5 s^4 + 1.35 s^3 + 2.25 s^2 + 0.3 s + 0.1
Continuous-time transfer function.
Wd1 =
s - 1
-------------------------------------
s^4 + 2.7 s^3 + 4.5 s^2 + 0.6 s + 0.2
Continuous-time transfer function.
Wd2 =
0.5 s^4 + 1.35 s^3 + 2.25 s^2 + 0.4 s
-------------------------------------------
0.5 s^4 + 1.35 s^3 + 2.25 s^2 + 0.3 s + 0.1
Continuous-time transfer function.
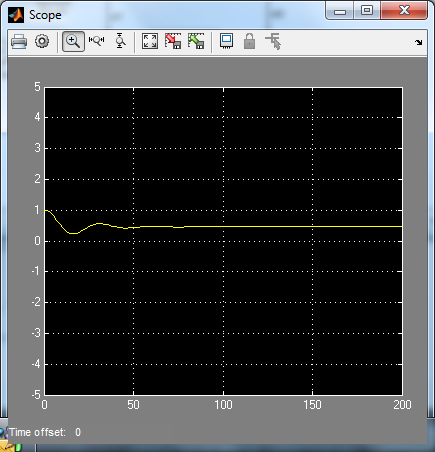
Caso e.1): r(t)=t, d1(t)=0.1, d2(t)=0.5
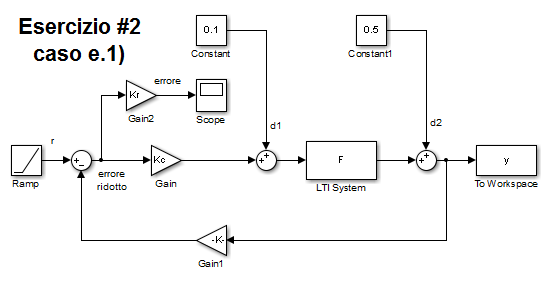
% errore intrinseco di inseguimento a r(t) = t pari a Kr/KGa = Kr/(Kc*Kf/Kr) % perché il sistema è di tipo 1 % effetto del disturbo d1 costante sull'uscita pari a d1/(Kc/Kr) perché ci sono poli % nell'origine solo nel blocco a valle del disturbo % effetto del disturbo d2 costante sull'uscita NULLO perché c'è almeno un % polo nell'origine nel blocco a monte del disturbo errore_r=dcgain(s*We*1/s^2) effetto_d1=dcgain(s*Wd1*0.1/s) effetto_d2=dcgain(s*Wd2*0.5/s) errore_tot=errore_r-(effetto_d1+effetto_d2) open_system('es_VI_2_1') sim('es_VI_2_1')
errore_r =
2
effetto_d1 =
-0.5000
effetto_d2 =
0
errore_tot =
2.5000
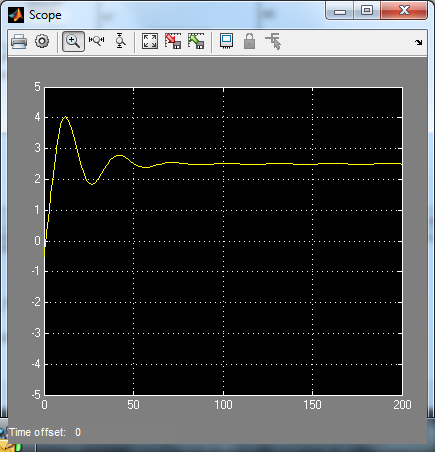
Caso e.2): r(t)=2, d1(t)=0.1, d2(t)=0.01t
% errore intrinseco di inseguimento a r(t) = 2 NULLO perché il sistema è di % tipo 1 % effetto del disturbo d1 costante sull'uscita pari a d1/(Kc/Kr) perché ci sono poli % nell'origine solo nel blocco a valle del disturbo % effetto del disturbo d2 = alfa_d2*t (rampa) sull'uscita pari ad alfa_d2/KGa = alfa_d2/(Kc*Kf/Kr) % perché il sistema è di tipo 1 errore_r=dcgain(s*We*2/s) effetto_d1=dcgain(s*Wd1*0.1/s) effetto_d2=dcgain(s*Wd2*0.01/s^2) errore_tot=errore_r-(effetto_d1+effetto_d2) open_system('es_VI_2_2') sim('es_VI_2_2')
errore_r =
0
effetto_d1 =
-0.5000
effetto_d2 =
0.0400
errore_tot =
0.4600