Laboratory 3 - Estimation, filtering and system identification - Prof. M. Taragna
Exercise 1: Parametric estimation of a resistance from current-voltage data stored in resistor_data_2.mat
Contents
Introduction
The program code may be splitted in sections using the characters "%%". Each section can run separately with the command "Run Section" (in the Editor toolbar, just to the right of the "Run" button). You can do the same thing by highlighting the code you want to run and by using the button function 9 (F9). This way, you can run only the desired section of your code, saving your time. This script can be considered as a reference example.
clear all, close all, clc
Procedure
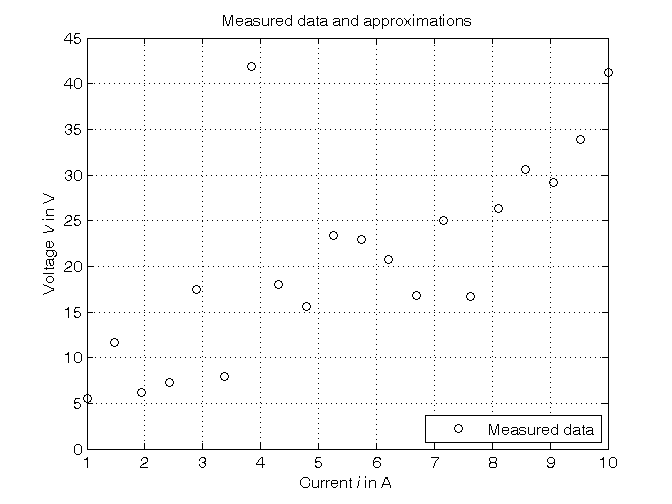
- Load the file resistor_data_2.mat containing the current-voltage data
- Plot the voltage measurements versus the current measurements
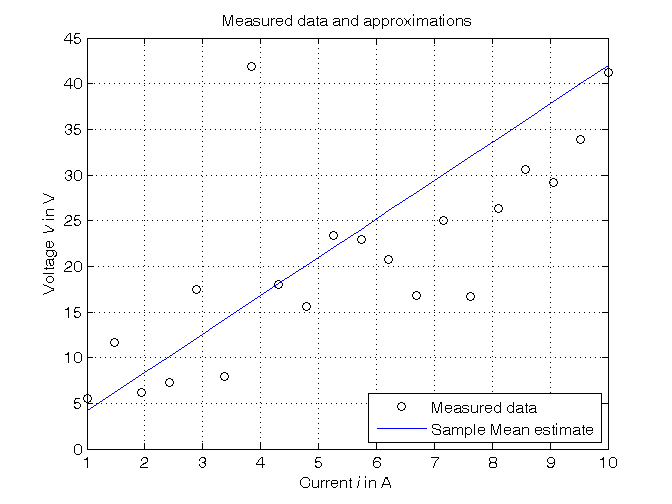
- Estimate the resistance using the Sample Mean algorithm
- Plot the estimated approximation versus the experimental data
- Define the noise variance matrix consistent with experimental data
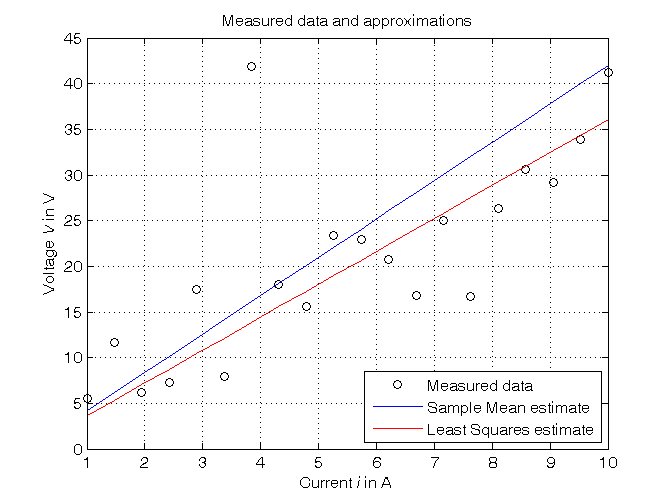
- Estimate the resistance using the Least Squares algorithm
- Plot the estimated approximation versus the experimental data
- Estimate the resistance using the Gauss-Markov algorithm
- Plot the estimated approximation versus the experimental data
- Estimate the resistance using the Bayesian method
- Plot the estimated approximation versus the experimental data
Problem setup
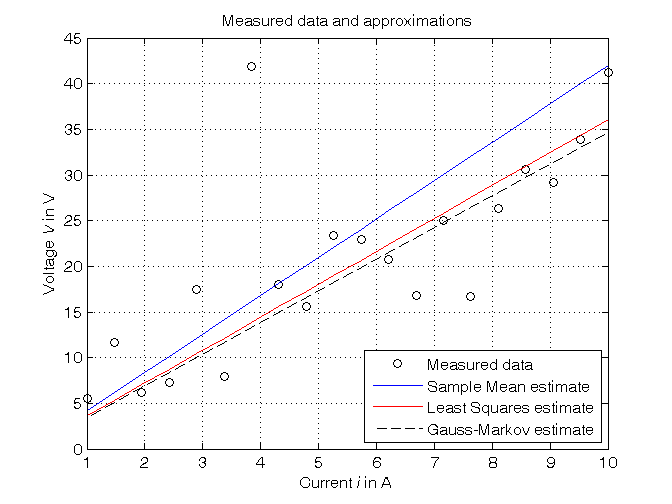
% Step 1: load of data load resistor_data_2.mat % i = current measured in Ampere % V = voltage measured in Volt N = length(i); % N = number of data % Step 2: plot of data figure, plot(i,V,'ok'), axis([min(i),max(i),0,45]), grid, title('Measured data and approximations'), xlabel('Current{\it i} in A'), ylabel('Voltage{\it V} in V'), legend('Measured data',4)
Estimation of the resistance using the Sample Mean algorithm
% Step 3: computation of the parameter estimate as mean of the R values % derived from the Ohm's law for each couple of current-voltage data R_SM = mean(V./i) % Form #1: using the "mean" operator R_SM_ = V'*(1./i)/N % Form #2: using the Sample Mean definition % Step 4: graphical comparison of the results V_SM = R_SM*i; figure, plot(i,V,'ok', i,V_SM,'-b'), axis([min(i),max(i),0,45]), grid, title('Measured data and approximations'), xlabel('Current{\it i} in A'), ylabel('Voltage{\it V} in V'), legend('Measured data','Sample Mean estimate',4)
R_SM =
4.1969
R_SM_ =
4.1969
Estimation of the resistance using the Least Squares algorithm
% Step 5: definition of the noise variance matrix consistent with data sigma_e = 5; Sigma_ee = sigma_e^2*eye(N); % Like with resistor_data_1.mat datafile % From data plot, the 7-th sample is not consistent with the others, % being highly corrupted. As a consequence, the weight of this sample % should be reduced. This can be obtained by forcing a high value of % the corresponding variance in the noise variance matrix, since each % variance represents the measure uncertainty: a larger variance reduces % the measure reliability. For example, instead of sigma_e^2 = 5^2, % the value (5*sigma_e)^2 = 25^2 can be forced. Sigma_ee(7,7) = (5*sigma_e)^2; % Step 6: computation of the parameter estimate Phi=i; R_LS=Phi\V % Form #1: using the "\" operator (more realiable) A=pinv(Phi); % more realiable than inv(Phi'*Phi)*Phi' R_LS_=A*V % Form #2: using the pseudoinverse matrix Sigma_R_LS = pinv(Phi)*Sigma_ee*pinv(Phi)' % Step 7: graphical comparison of the results V_LS = R_LS*i; figure, plot(i,V,'ok', i,V_SM,'-b', i,V_LS,'-r'), axis([min(i),max(i),0,45]), grid, title('Measured data and approximations'), xlabel('Current{\it i} in A'), ylabel('Voltage{\it V} in V'), legend('Measured data','Sample Mean estimate','Least Squares estimate',4)
R_LS =
3.6070
R_LS_ =
3.6070
Sigma_R_LS =
0.0487
Estimation of the resistance using the Gauss-Markov algorithm
% Step 8: computation of the parameter estimate % Note that the Gauss-Markov estimate differs from the Least Squares % estimate when different weights are used for the measurements R_GM = inv(Phi'*inv(Sigma_ee)*Phi)*Phi'*inv(Sigma_ee)*V Sigma_R_GM = inv(Phi'*inv(Sigma_ee)*Phi) % Step 9: graphical comparison of the results V_GM = R_GM*i; figure, plot(i,V,'ok', i,V_SM,'-b', i,V_LS,'-r', i,V_GM,'--k'), axis([min(i),max(i),0,45]), grid, title('Measured data and approximations'), xlabel('Current{\it i} in A'), ylabel('Voltage{\it V} in V'), legend('Measured data','Sample Mean estimate','Least Squares estimate',... 'Gauss-Markov estimate',4)
R_GM =
3.4673
Sigma_R_GM =
0.0338
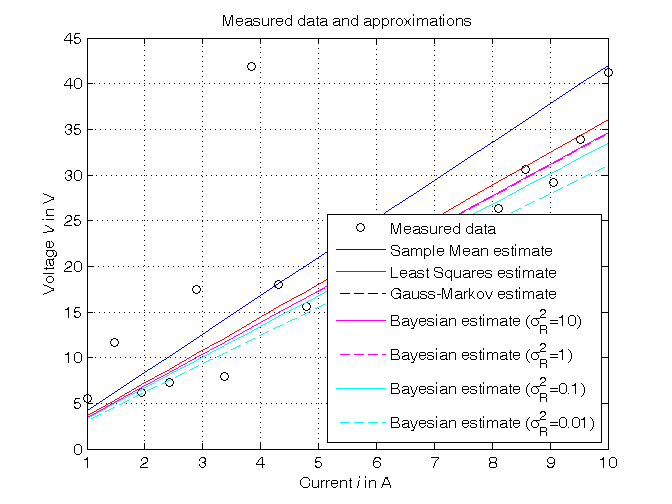
Estimation of the resistance using the Bayesian method
% Step 10: computation of the parameter estimate, assuming: % - R_bar = a priori mean value of R = 3 (to be assumed early) % - Sigma_RR = a priori variance of R = 10, 1, 0.1, 0.01 (to be assumed early) % - V_bar = mean value of V = R_bar*i % - Sigma_VV = Sigma_RR*i*i' + Sigma_ee % - Sigma_RV = Sigma_RR*i' R_bar = 3; % Try also with R_GM Sigma_RR = [10, 1, 0.1, 0.01]; V_bar = R_bar*i; for k=1:length(Sigma_RR), Sigma_VV = Sigma_RR(k)* i*i' + Sigma_ee; Sigma_RV = Sigma_RR(k)*i'; R_B(k) = R_bar + Sigma_RV * inv(Sigma_VV) * (V-V_bar); Sigma_R_B(k) = Sigma_RV * inv(Sigma_VV) * Sigma_RV'; % estimate variance Sigma_R_minus_R_B(k) = Sigma_RR(k) - Sigma_R_B(k); % a posteriori variance V_B(:,k) = R_B(k)*i; end Sigma_RR, R_B, Sigma_R_B, Sigma_R_minus_R_B % Step 11: graphical comparison of the results figure, plot(i,V,'ok', i,V_SM,'-b', i,V_LS,'-r', i,V_GM,'--k', ... i,V_B(:,1),'-m', i,V_B(:,2),'--m', ... i,V_B(:,3),'-c', i,V_B(:,4),'--c'), axis([min(i),max(i),0,45]), grid, title('Measured data and approximations'), xlabel('Current{\it i} in A'), ylabel('Voltage{\it V} in V'), legend('Measured data','Sample Mean estimate','Least Squares estimate',... 'Gauss-Markov estimate', ... ['Bayesian estimate (\sigma_R^2=', num2str(Sigma_RR(1)),')'], ... ['Bayesian estimate (\sigma_R^2=', num2str(Sigma_RR(2)),')'], ... ['Bayesian estimate (\sigma_R^2=', num2str(Sigma_RR(3)),')'], ... ['Bayesian estimate (\sigma_R^2=', num2str(Sigma_RR(4)),')'],4)
Sigma_RR =
10.0000 1.0000 0.1000 0.0100
R_B =
3.4657 3.4520 3.3493 3.1067
Sigma_R_B =
9.9663 0.9673 0.0747 0.0023
Sigma_R_minus_R_B =
0.0337 0.0327 0.0253 0.0077